How Ungrading Enriches Test Prep and Accelerated Courses

Using LPM in test prep, Gifted & Talented, Advanced Placement, and International Baccalaureate programs.

Introduction

Teaching an accelerated course, especially one tied to high-stakes testing, comes with a unique set of pressures. I used to be frustrated by the demands of teaching Advanced Placement—feeling like the relentless pace and grading took the joy out of learning. I even stepped away from it for a while because I couldn’t see how to apply an ungraded approach. But over time, I’ve realized it doesn’t have to be that way. It’s possible to keep the focus on learning and growth, ungrading while still preparing students for the rigor of a specific, points-based exam. Whether you’re navigating state testing (such as Regents exams), IB (International Baccalaureate), AP (Advanced Placement) programs, or a Gifted and Talented (G&T) program, you can create an environment that prioritizes deep, meaningful learning rather than just teaching to the test. Ungrading enriches test prep and accelerated courses.

In my own journey, teaching AP Physics has been my primary focus. While this article draws on my experience in that specific subject, the strategies I’ll share are easily adaptable to any accelerated class or statewide test prep, across subjects and age groups. I’m going to walk you through how I approached the newly revised grading criteria for AP and used them as a foundation to develop learning progressions that foster content mastery, critical thinking, and creativity.

I invite you to join me in this process—share your thoughts and offer feedback—let’s work together to refine our ungrading approaches. After all, we’re all navigating the evolving landscape of education, and there’s power in collaboration. So, stick around—let’s dive into strategies that will help us bring the joy of learning back into high-stakes teaching while empowering our students to thrive.

Setting the Stage: What sets these programs apart

Distinguishing between the various exams and programs

In today’s competitive academic landscape, students often turn to programs like AP (Advanced Placement) and IB (International Baccalaureate) for academic challenges, college credit, and enhanced admissions prospects. AP courses, primarily U.S.-centric, focus on individual subjects and include both multiple-choice and free-response exams, often using rubrics for evaluation in subjects like history and English (College Board, 2024). IB, with a global reach, emphasizes a holistic, interdisciplinary approach, relying on essays, research projects, and problem-solving tasks (International Baccalaureate, 2024).

G&T (Gifted and Talented) programs, typically at the elementary and middle school levels, cater to high-achieving students with a differentiated curriculum aimed at fostering creativity and higher-order thinking (Corwith, 2019). Additionally, many high schoolers prepare for college entrance exams like the SAT and ACT, which are essential for college admissions and scholarships. Some schools now integrate SAT/ACT prep into their curriculum due to the increasing importance of these exams (PrepScholar, 2023).

Finally, state testing can have a huge influence on educational experiences, as passing standardized tests is often mandatory for graduation, with results sometimes influencing teacher evaluations This tends to narrow the curriculum, constricting time left for creative and authentic learning (Au, 2007; Kohn, 2007).

All of these programs can benefit from an ungrading approach, which shifts the focus toward authentic learning and continuous improvement rather than traditional grading.  Methods such as the Learning Progression Model, encourage students to demonstrate mastery of content and skills over time, fostering a deeper understanding and better preparation for success on standardized tests. By emphasizing growth and meaningful feedback, ungrading enriches test prep and accelerated courses by having students engage with material more fully, while still preparing them for the assessments required by AP, IB, and other testing-based programs. 

Why Students Enroll in these programs

One of the main reasons students enroll in accelerated programs like AP or IB is the chance to earn college (or high school) credits and secure advanced placement. High scores on IB and AP exams are recognized by many colleges and universities worldwide, enabling students to reap several benefits. First, they can earn college credits, which may satisfy general education or prerequisite courses, reducing the number of classes needed for a degree. Second, students can skip introductory courses, allowing them to dive into more advanced subjects or focus on their major earlier in their academic careers. Lastly, this can lead to tuition savings, as fewer required courses often result in shorter time spent in college, lowering overall costs.

Both IB and AP programs offer rigorous academic experiences that prepare students for the challenges of higher education. Similarly, G&T (Gifted and Talented) programs in middle schools help prepare students for high school, especially if they are targeting specialized or selective programs that may require entrance exams. These accelerated courses, however, can be difficult to navigate when a “gradeless” approach is desired. Often, teachers have little control over the final exams, especially in AP or IB, so they need to ensure that students understand how the grading system works, whether it’s points-based or rubric-based.

In contrast, G&T programs, which typically do not have standardized external exams, present their own challenges, particularly in grading subjective areas such as creativity or problem-solving. Regardless of the program, the ultimate goal is to ensure that students are learning advanced material above their grade level. Students who earn placement or credit through these programs must retain a solid understanding of the content to succeed in subsequent, more challenging courses. For example, if a middle school student places out of Algebra 1 after completing a G&T program, they must have a firm grasp of Algebra 1 concepts to perform well in Algebra 2.

I believe that Learning Progressions, when used alongside traditional testing and scoring systems, can provide a balanced approach. They help students develop transferable skills and ensure that they have truly mastered the material at a high level, going beyond just test preparation and fostering long-term academic success.

A Specific Example: AP Physics

My Context

Last year, I taught AP Physics 1 for the first time since 2021. As I have written about here and here, I used the Learning Progression Model to assess my students and it worked extremely well, even better than I expected. Using the first eight of the learning progressions from the Physics LPs, I only omitted 2 and added one new AP-specific LP to adapt to the specific requirements of the Advanced Placement course.

However, by the end of the year, I found that some of the descriptors in my rubric did not quite match what my students needed to be able to do. For example, graph interpretation on the Free Response Questions (FRQs) is generally qualitative, rarely requiring the interpretation of the mathematical model, which is a requirement as written in my Graph Interpretation’s Advanced and Expert levels. 

Because of issues like this, I was already planning to revise my rubric. And then, the Advanced Placement program came out with their revisions for 2024-2025. This included reducing the Science and Engineering Practices (SEPs) to 3 from 7, the number of MCQs to 40 from 50, and the number of FRQs to 4 from 5 (College Board 1, 2024). To better align my scoring with the new criteria, I decided to write completely new learning progressions for AP Physics. While these would apply to AP Physics 1, 2, and C, I would be testing it out only with AP Physics 2 this year.  

What the new AP Practices are

The AP Physics program made several revisions in unit and topic sequencing, uncoupling specific science practices from specific learning objectives, and quantities/types of questions on the test. (College Board 2, 2024) But most importantly for this essay, they revised the science practices.

First, let’s look at what the AP program published. All of this information can be found in the AP® Physics 1: Algebra-Based course and exam description, which can be downloaded. Figure 1 shows the 3 practices and the component skills for each. Note that All AP Physics courses (1, 2, & C) use the same practices. 

Figure 1 AP Practices (image excerpted from AP physics 1: Algebra-based, COURSE AND EXAM DESCRIPTION, 2024)

I have to understand what the practice is and how students will be required to show evidence of it. After reading the thorough descriptions, here’s what I understand about the Modeling, Problem Solving, and Data Analysis & Claims practices.

Practice 1: Modeling

Students learn to simplify complex real-world systems by creating models, which can be conceptual (like viewing electric current as flowing particles) or mathematical (such as Ohm’s law). These models help explain and predict phenomena. Whether it’s simplifying a system to a single object or analyzing multiple interacting objects, students must recognize which features are most important. Visual representations—like graphs, diagrams, and charts—are key tools for helping students analyze and communicate these ideas. They are also taught to avoid common misconceptions, such as assuming all data must fit a linear pattern, and instead focus on accurately constructing best-fit curves.

Practice 2: Problem Solving

Students use mathematical representations to connect physical concepts to the equations that describe them. The goal is to go beyond just plugging numbers into formulas and instead understand when and why certain equations apply. By first describing problems in multiple ways (e.g., using force diagrams or sketches), students can better choose the correct mathematical approach. They are encouraged to manipulate the algebraic form of equations before substituting values, ensuring that their results are meaningful in terms of units and real-world context. Additionally, students must connect mathematical relationships (like proportionality) to cause-and-effect scenarios in the physical world.

Practice 3: Data Analysis and Claims

Students analyze data to develop claims about physical phenomena, forming arguments backed by evidence. The design and refinement of experiments are central to this practice, especially in handling measurement uncertainty and recognizing the limits of the data. While AP Physics 2 doesn’t require in-depth error analysis, students should estimate percent errors and understand how to minimize uncertainty. As they encounter new data, students should revise their explanations and improve their methods, ensuring their conclusions are well-supported. Encouraging them to collect and analyze their own data deepens their understanding and engagement with the course material.

Together, these practices aim to cultivate the analytical and reasoning skills necessary for students to handle advanced problems in physics, preparing them for both academic and real-world applications.

The structure and goals of the exam

In all AP Physics courses, students are evaluated through four main types of questions, each designed to assess different skills that physicists use in real-world problem-solving. Again, all of this information can be found in the AP® Physics 1: Algebra-Based course and exam description. Here’s how each type of question works:

  • Mathematical Routines (MR) focuses on students’ ability to use mathematics to analyze and predict outcomes in a physical scenario. Students are expected to derive relationships between variables and calculate numerical values. In addition, they must support their mathematical analysis with appropriate physics concepts, making logical connections between different ideas.
  • Translation Between Representations (TBR) tests students’ capacity to move between different forms of representing a scenario, such as diagrams, graphs, and equations. Students must justify how their visual and mathematical representations relate to each other, and often predict how changes in the scenario would affect these representations.
  • Experimental Design and Analysis (LAB) assesses students’ ability to develop scientifically sound experiments and analyze data. Students are tasked with designing an experiment that could be performed in a high school lab, considering factors like varying one parameter and measuring its effect on another. They are then given experimental data to analyze, using tools such as graphs to draw conclusions about the physical quantities involved.
  • Qualitative/Quantitative Translation (QQT) requires students to connect the physical concepts, mathematical equations, and nature of the scenario. They must make a claim about the scenario, derive related equations, and justify whether their mathematical answers align with their qualitative reasoning. This question focuses on understanding how changes to the scenario would alter the mathematical or conceptual representations.

Each question type challenges students to integrate physics concepts with mathematical reasoning, encouraging them to think critically and holistically about the physical world. The goal is not just to solve problems but to explain and justify their reasoning at every step. This approach mirrors the methods used by physicists to understand complex phenomena.

Evaluating the Practices Using the Question Types

While the questions are distinct, there is a lot of overlap between the questions and the practices. All except practices 1A, 1B, and 3A have two or more questions that they are evaluated in. See Figure 2.

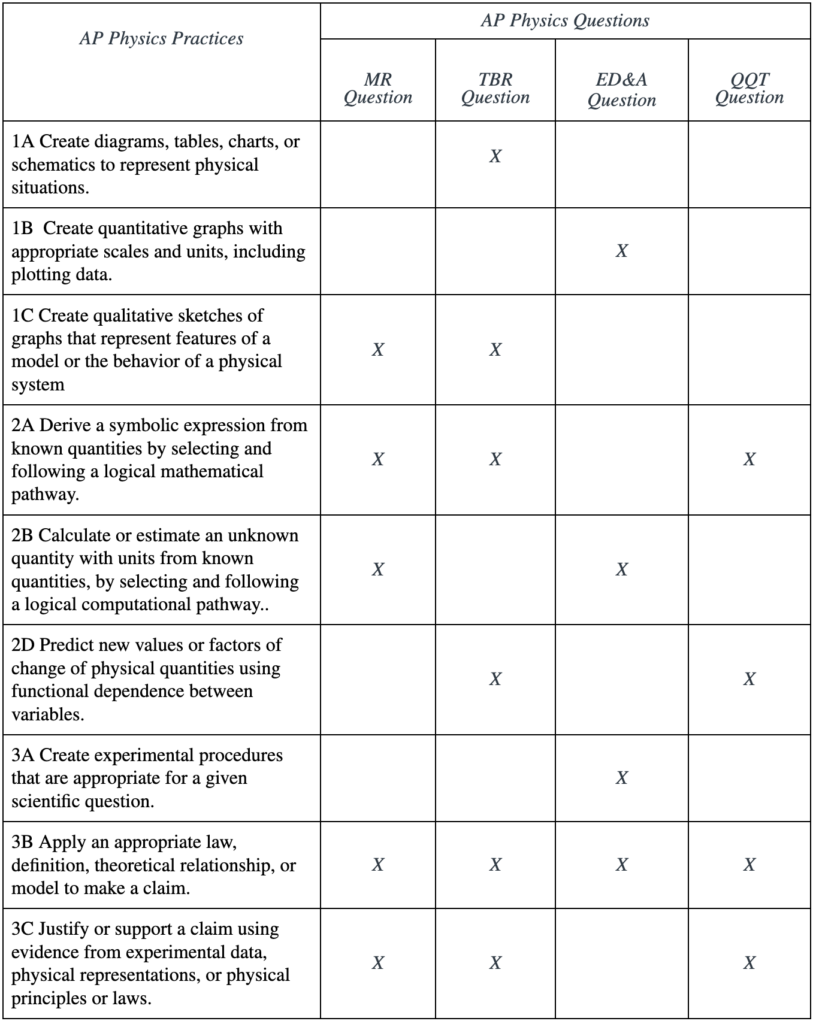
Figure 2: Subpractices embedded in SEPs

The repetition of the practices across multiple question types creates unnecessary complexity in the evaluation process, in my opinion. While I understand that AP aims to maintain flexibility in their assessments, this approach leads to what feels like double jeopardy—evaluating students multiple times on the same practice. This not only increases the workload but also complicates the feedback process. In my experience, it’s more efficient to assess a skill once, providing targeted feedback rather than repeating the same assessment across different types of questions. (Remember, with LPM, each practice will be reassessed at the end of each unit, so they have multiple attempts to succeed.)

For this reason, I’ve decided not to organize my Learning Progressions (LPs) based on the three overarching practices that AP uses. Though the idea of using the nine sub-practices might seem like a solution, they too have significant overlap, which I find unnecessary. Instead, I prefer to structure my assessments by question type: four distinct problems, four distinct practices.

This approach allows me to focus on the key facets of each problem type. For example, if 3B (applying an appropriate law) is a component of all four questions, I decide on which one I will make it the primary focus. This is something I’ve already been doing—selecting what to emphasize in my feedback to make sure the evaluations remain clear, distinct, and easy for students to use.

Additionally, I believe that the language of the practices, as written for educators, needs to be simplified for students. To make the focus of each learning progression clear and accessible, I rewrote and rearranged the practices in student-friendly language. This ensures that students can easily understand the criteria and objectives, making the learning process more transparent and effective.

My Four Practices Adapted from the AP Physics Practices and Question Types

Here are my four practices as described to students in the grading document that I provide for them at the beginning of the school year.

  • Modeling: The goal of modeling is to create representations that accurately depict physical phenomena. General examples include labeled sketches, diagrams, tables, charts, schematics, and both qualitative and quantitative graphs. In physics, specific models might involve force diagrams, energy bar charts, ray diagrams, or circuit diagrams. You are expected to connect different representations of the same scenario. Note: This practice focuses on modeling as an end goal. If the model supports mathematical analysis, it will be evaluated under the “Solving Problems” practice.
  • Solving Problems: This practice focuses on using mathematical representations to derive, calculate, estimate, or predict scientific phenomena. These representations include numbers, symbols, algebraic expressions, and equations. Problem-solving demonstrates how physics concepts interrelate and the logical steps taken to reach a solution. Generally, this involves identifying givens and variables, labeling sketches, creating diagrams (e.g., free-body diagrams, bar charts), selecting equations, inserting values, and arriving at a final answer with correct units. Note: When modeling supports mathematical problem-solving (e.g., free-body diagrams), it will be assessed here. If modeling stands alone, it will be scored under “Modeling.”
  • Asking Scientific Questions: This practice involves describing experimental procedures and analyzing data. You must be able to formulate relevant questions, design and conduct procedures, and recognize the assumptions and limitations of your experiments. Well-structured questions should be specific, feasible with available resources, and should lead to clear observations or conclusions. Data analysis may include calculations, theoretical derivations, error analysis, and responses to discussion questions. Note: Graph creation and interpretation are evaluated under the “Modeling” practice.
  • Creating an Argument: The goal here is to construct a persuasive and meaningful argument, using evidence to support your claim. This might include definitions, laws, mathematical models, equations, or relationships from current or previous study units in physics. The argument should logically link the evidence to the claim, demonstrating your understanding of the underlying concepts.

With only four practices, I can score each of the four question types using only one of my practices. Will I be evaluating every facet of the AP question? No, I will only give feedback on the section or aspect that the practice asks about. Figure 3 shows how I am planning to evaluate each of the practices using AP question types. Modeling will be assessed on the TBR question, Solving problems on the QQT question; Asking Scientific Questions on the ED&A question, and Creating an argument on either the MR or ED&A question depending on the context.

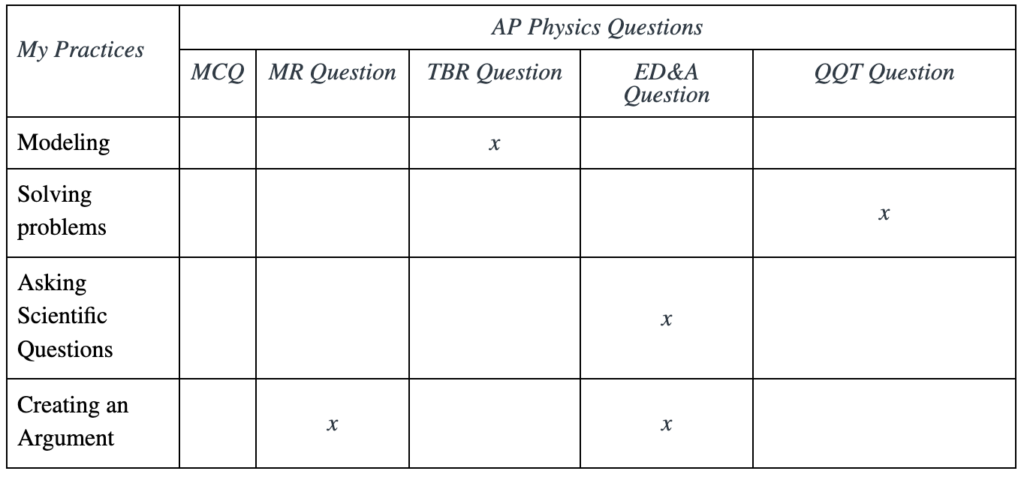
Figure 3: Intersection of my practices with AP Questions

That might leave you wondering about how I will evaluate the rest of the AP questions: the parts of the FRQs not scored by the practice and all of the MCQs. For that, I will continue to use the AP Test Practice LP that I used last year, which worked extremely well.  This AP Test Practice is described as “The goal is to increase your test-taking abilities specifically for the AP Physics exam. This means that you complete the Personal Progress Checks (MCQ) and (FRQ) for each unit accurately, according to their scoring requirements, and improve your AP score.” This provides feedback to students about how well they are preparing for the actual exam, correlated to the AP exam scoring.

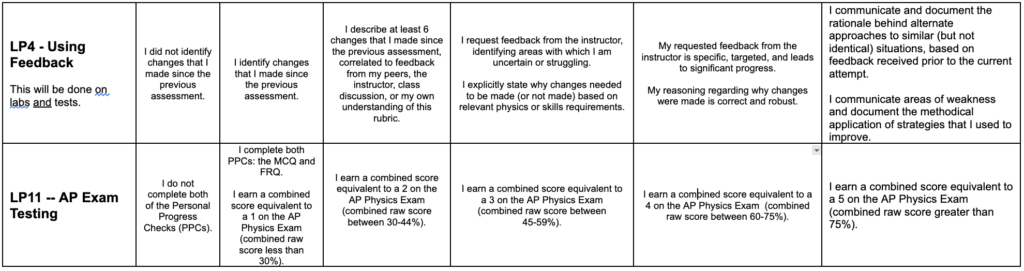
Last but not least, what about experimentation? It is a huge component of the AP Physics program. In my other classes, as well as last year in AP Physics 1, I used 4 practices to score labs: Experimental Design, Data Analysis, Arguing a Claim, and Using Feedback. After much thought, I have decided that I can evaluate the first three of those with the new practices that I have already developed. Experimental Design = Asking Scientific Questions, Data Analysis = Modeling, Arguing a Claim  = Creating an Argument. I think it will be very useful to evaluate students on the same practices in different formats, on a lab report or activity documentation as well as in a test situation. It will give them that many more times to get feedback. 

The only thing missing is Using Feedback. I have been successfully using this practice for years and students find it very valuable. The using feedback section is where students annotate their work, highlighting the changes  made from the previous assessment of its type. The goal is to communicate what changes made, why they made them, and how they have improved over time. I have altered the wording slightly (“work” instead of “lab reports” to provide more flexibility. I may want to use it for other types of assessment in addition to lab reports.)

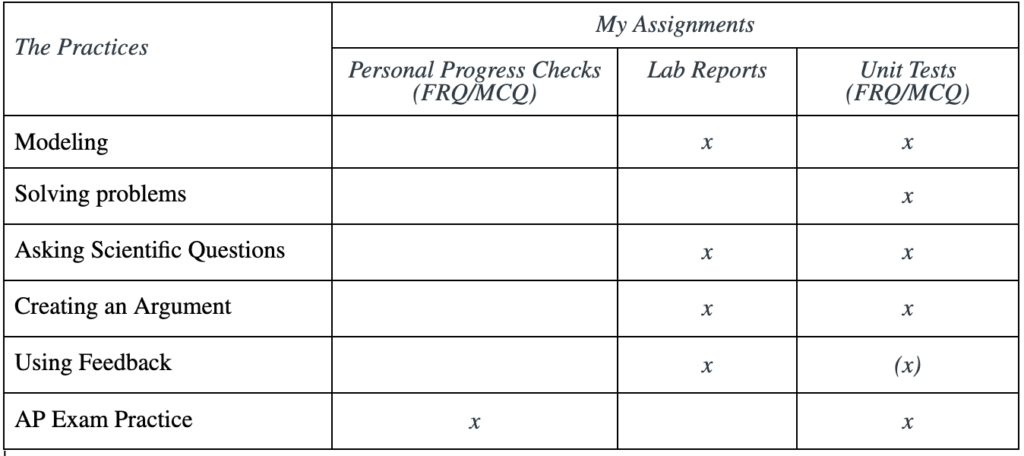
Figure 4 shows how I am planning to use each of the practices. On lab reports and activities, of which there are at least 3 per unit, they will get feedback on Modeling, Asking Scientific Questions, Creating an Argument and Using Feedback. On personal progress checks (PPCs; AP’s name for end-of-unit reviews), checkpoints (quizzes) and unit tests, they will get feedback on Modeling, Solving problems, Asking Scientific Questions, Creating an Argument, and AP Test Practice. There is one PPC, 1-3 checkpoints, and 1 unit test each unit. They should get tons of feedback, whether from me directly, from peer review, or self-assessment. There are 7 units which means a total of 20 labs/activities, 7 PPCs and Unit Tests, and anywhere between 10-15 checkpoints.

Figure 4: How my assignments use the practices

Creating the new Learning Progressions

OK, so now I have 6 practices (down from 9 last year). They are clearly worded and I understand how I will use them. Next, I need to develop the Learning Progressions. I began with the AP question descriptions, honing the language and focusing the descriptors. I used color coding to show how the skills are threaded across the levels, maintaining consistency and providing developmentally-appropriate guidance.

Let’s go through them one by one.

The color coding is important, as it shows how I am pulling the individual component skills through the levels. For example, the red text tracks the creation of the model itself, usually a graph. The blue text is about the content of the model, such as labeling the axes and including a trendline. Green is content-specific explanations. Purple is pushing students to use advanced analysis methods. Since this is new for myself and the student, I also included clarifying notes under the rubric itself. Note 2 (referenced in Advanced) says: “Advanced analysis methods include linearization of the graph and/or interpretation of the mathematical model”. Pink is about being able to use the model to generate something new. This too is accompanied by a clarifying note: “There are many possible applications of the representations, including but not limited to generating data, supporting explanations, making predictions, analyzing sensitivity of systems and/or reconciling divergent outcomes.” Remember, the assignment description will have the specific information about the requirements for that particular assessment. That information does not need to be specified in the rubric itself.

OK, let’s do the same for the remaining learning progressions. The colors do not have the same meanings as they did in the Modeling practice, but they do track the various components needed to succeed for each individual practice. 

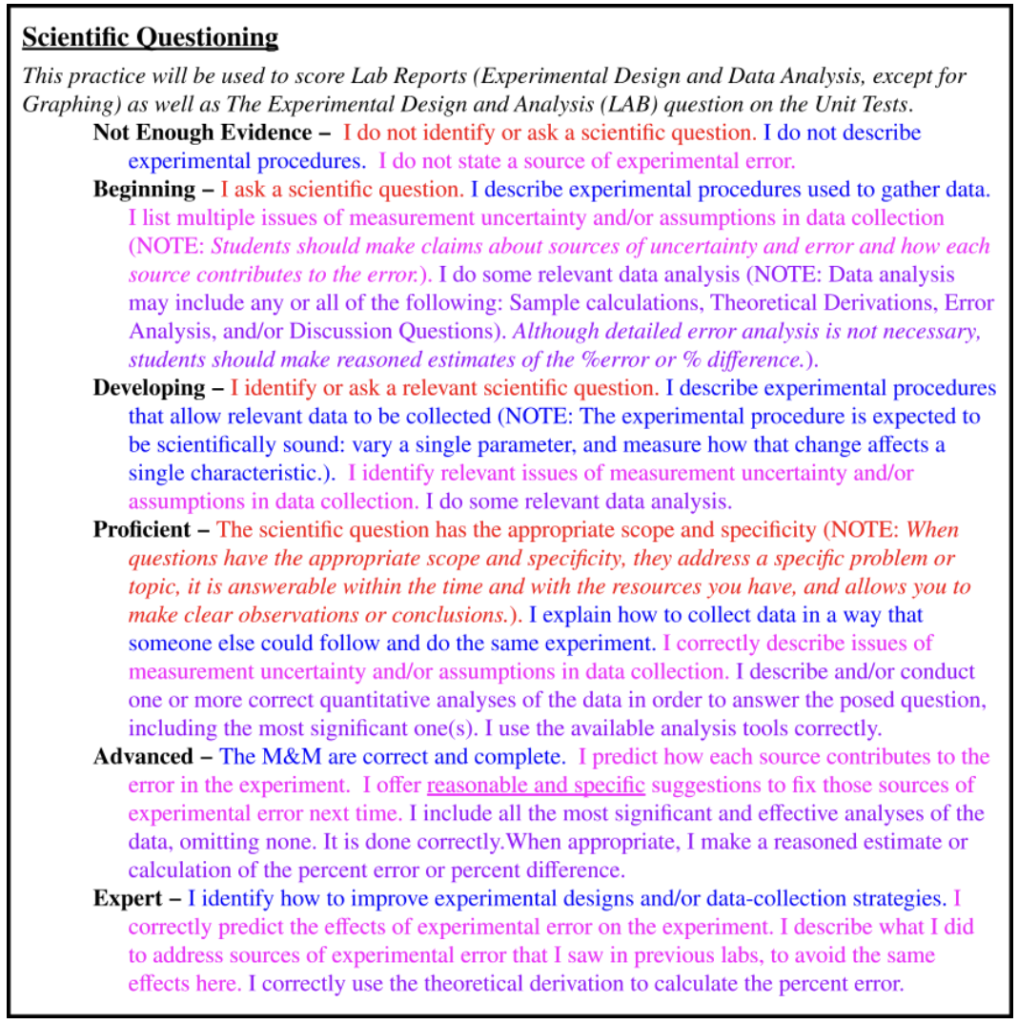
In this post, to ease reading, I have been using lists to display the learning progressions. However, this is not how I give them out to students or use them on assessments. Generally, I use a traditional rubric table that looks like this:

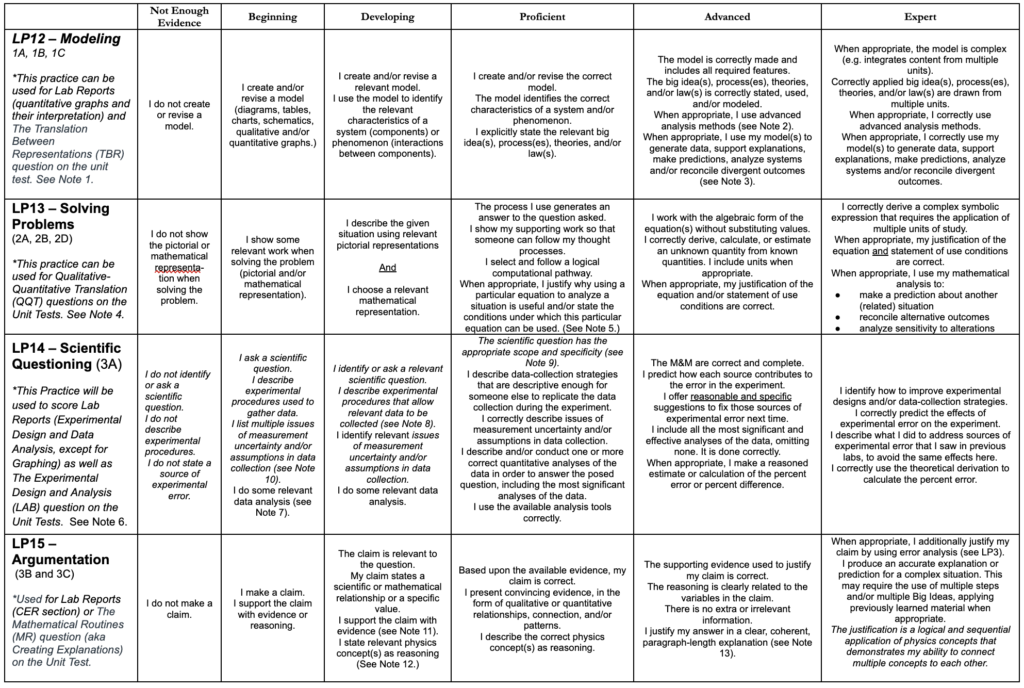
  • NOTE 1: This practice is for modeling that is the end in and of itself. When the models are specifically used to support mathematical representations, they will be scored using Practice 2.
  • NOTE 2: Advanced analysis methods include linearization of the graph and/or interpretation of the mathematical model
  • NOTE 3: There are many possible applications of the representations, including but not limited to generating data, supporting explanations, making predictions, analyzing sensitivity of systems and/or reconciling divergent outcomes.
  • NOTE 4: This practice includes modeling (pictorial representations like labeled sketches, free body diagrams, schematics, etc) that is/are specifically used to support mathematical representations. When modeling is the end in and/of itself, they will be scored using Practice 1.
  • NOTE 5: Stating the conditions under which the equation can be used includes limits (“only when acceleration is zero”, “only for an isolated system”) and/or assumptions (“assuming force is held constant”). 
  • NOTE 6: Evaluation of Graph Creation and Interpretation will be done using Practice 1. 
  • NOTE 7: Data analysis may include any or all of the following: Sample calculations, Theoretical Derivations, Error Analysis, and/or Discussion Questions). Although detailed error analysis is not necessary, students should make reasoned estimates of the %error or % difference.
  • NOTE 8: The experimental procedure is expected to be scientifically sound: vary a single parameter, and measure how that change affects a single characteristic.
  • NOTE 9: When questions have the appropriate scope and specificity, they address a specific problem or topic, it is answerable within the time and with the resources you have, and allows you to make clear observations or conclusions.
  • NOTE 10: Students should make claims about sources of uncertainty and error and how each source contributes to the error. 
  • NOTE 11: Evidence may be qualitative or quantitative. Depending on the experiment or question, this may involve relationships, connections, and/or patterns in the data or analysis. Students need to provide/use the most sophisticated evidence available at the time. (See the Hierarchy of Evidence.)
  • NOTE 12: Physics concepts may be theories, laws, definitions, or relationships. Equations may be used as support for a concept, but are insufficient alone.
  • NOTE 13: For AP Physics 1 and 2 exams, the MR question will ask students to make a claim or prediction about the scenario and use appropriate physics concepts and principles to support and justify that claim.

The font is so small! I hope you can see why I presented it the way I did. Regardless, if you would like access to this document to either use in your class or edit to create your own, please send me an email. I’m happy to share!

Concerns and Challenges

I have concerns about the complexity and wordiness of the language, specifically in Scientific Questioning and Argumentation. This stands out particularly when it comes to ensuring students can consistently achieve higher proficiency levels like Advanced or Expert. These practices, as currently written, tend to involve multiple steps, which can feel overwhelming and unclear, making it harder to design assessment questions that effectively target these levels.

 

That said, I realize perfection isn’t required from the start. Just as I encourage my students to make mistakes and learn from feedback, I need to allow myself the same grace. As I begin applying these practices in real assessments, I’ll be able to refine and adjust them based on how students perform and what kind of feedback they need. Over time, I expect to find simpler ways to communicate expectations without compromising the high level of performance. To manage this over the school year, I plan to simplify and clarify the language whenever possible. By testing the practices in assessments, I’ll see which parts work and which cause confusion, allowing me to adjust them to better align with students’ needs. After the first assessment alone, I already see that I need to add qualifiers like “When appropriate” and “and/or” to some of the descriptors.

On the AP exam, FRQs have multiple parts addressing different aspects of various practices. Likewise, I can break my questions down into smaller, more manageable components to help students navigate the new learning progressions. As I refine my rubrics and practices, I’ll focus on tracking student progress and engagement with the core skills, like asking relevant questions or constructing clear arguments. This will guide me in identifying what needs to be explicitly clarified in both assignments and learning progressions.

Under the crucible of use, I will be able to refine the language, fine tuning as I apply them to specific questions on assessments.  Although it may take some time, the language of these practices will naturally evolve, becoming more practical and manageable in the long run. Every new learning progression I’ve written has revealed cracks once I’ve used it with students, and I expect the same here. However, I don’t mind this iterative process—I’m teaching AP Physics 2 this year. All of my students had me in AP Physics 1 or Honors Physics last year. They were successful, and understand the LPM.  With transparency, I plan to involve them in refining these practices, explaining the purpose behind it. I know they’ll be on board and willing to help me learn and grow.

I’m not going to deceive you. Over the summer, I was vacillating about whether or not to use these new practices. I already have a lot on my plate this year. On top of that, I’m not sure if I’ll be teaching this course again next year, so it feels like a lot of work for a class I may not teach again. I also no longer have colleagues at my school to collaborate with, leaving me to navigate this on my own. It would be incredibly helpful to have a second or third set of eyes on this—any volunteers? That’s why I’m sharing this process publicly; together, we can improve and refine these ideas.

Conclusion

While the practices I’ve outlined are tailored specifically for AP Physics, the approach I’m taking can easily be adapted to any accelerated or test-centric program—whether it’s IB, honors courses, or gifted and talented programs. The key takeaway is that regardless of the subject, refining learning progressions to provide clear, actionable feedback is essential for helping students reach their full potential. By simplifying and adjusting language, we can ensure that students not only understand the expectations but are also able to achieve higher levels of proficiency in a structured, meaningful way.

This approach can be especially valuable for teachers navigating the balance between test preparation and maintaining a rich, interesting curriculum. By focusing on authentic learning and providing meaningful feedback, teachers can encourage students to engage deeply with the material, rather than simply memorizing facts for the exam. For example, ungrading strategies or a focus on learning progressions help shift the emphasis toward skill development and critical thinking, which not only prepares students for exams but also enhances their overall learning experience. Using a “Test Prep” learning progression is an effective way to offer feedback on students’ test-taking strategies and overall progress, treating external scores as just one of many valuable learning experiences in your class. This approach allows you to focus on developing skills that are essential for both exam success and broader academic growth, while still integrating meaningful assessments that go beyond just the test results. This way, teachers can integrate test prep organically without sacrificing the exploration of interesting, complex topics that make the course engaging and relevant. By weaving test preparation into a curiosity-driven approach, students become better equipped to succeed on their exams while remaining invested in the subject matter.

That said, I realize perfection isn’t required from the start. Just as I encourage my students to make mistakes and learn from feedback, I need to allow myself the same grace. As I begin applying these practices in real assessments, I’ll be able to refine and adjust them based on how students perform and what kind of feedback they need. Over time, I expect to find simpler ways to communicate expectations without compromising the high level of performance. To manage this over the school year, I plan to simplify and clarify the language whenever possible. By testing the practices in assessments, I’ll see which parts work and which cause confusion, allowing me to adjust them to better align with students’ needs. After the first assessment alone, I already see that I need to add qualifiers like “When appropriate” and “and/or” to some of the descriptors.

On the AP exam, FRQs have multiple parts addressing different aspects of various practices. Likewise, I can break my questions down into smaller, more manageable components to help students navigate the new learning progressions. As I refine my rubrics and practices, I’ll focus on tracking student progress and engagement with the core skills, like asking relevant questions or constructing clear arguments. This will guide me in identifying what needs to be explicitly clarified in both assignments and learning progressions.

If you’re interested in exploring how these ideas might work in your classroom or program, I encourage you to comment below with your thoughts, contact me personally via email to collaborate, or subscribe to my newsletter for regular updates on best practices in education. 

Additionally, don’t miss the opportunity to dive deeper into the Learning Progression Model by buying (or recommending) my latest book, The Learning Progression Model, available on Amazon in paperback, hardcover, ebook, or (coming soon) audiobook. Together, we can improve the educational experience for students in advanced programs and create a more meaningful, impactful learning journey.

Elise Naramore's published book on assessment in education

References

AP physics 1: Algebra-based. AP Physics 1: Algebra-Based Course – AP Central | College Board. (2024). https://apcentral.collegeboard.org/courses/ap-physics-1 

Au, W. (2007). High-stakes testing and curricular control: A qualitative metasynthesis.

Educational Researcher, 36(5), 258-267. https://doi.org/10.3102/0013189X07306523

College Board. (2024). AP physics 2: Algebra-based. AP Physics 2: Algebra-Based Course – AP Central | College Board. https://apcentral.collegeboard.org/courses/ap-physics-2  

College Board. (2024). AP physics 2: Algebra-based. AP Physics Revisions for 2024-25. https://apcentral.collegeboard.org/courses/ap-physics/revisions-2024-25  

College Board. (2024). Course and Exam Pages. https://apcentral.collegeboard.org/courses

Corwith, S. (Ed.). (2019). NAGC Pre-K-Grade 12 gifted programming standards. National Standards in Gifted and Talented Education. https://nagc.org/page/National-Standards-in-Gifted-and-Talented-Education

International Baccalaureate Organization. (2024). International Education – International Baccalaureate®. https://www.ibo.org/. https://www.ibo.org/ 

Kohn, A. (2000). The case against standardized testing: Raising the scores, ruining the schools. Heinemann.

Please consider buying or recommending my latest book, The Learning Progression Model, available on Amazon in paperback, hardcover, ebook, or (coming soon) audiobook.

Elise Naramore's published book on assessment in education